题解 4.21模拟赛T4

发表于 | 更新于

$Description$

$Ahri$得到了一个$(h+1) × (w+1)$的巧克力，这意味着她横着最多可以切$h$刀，竖着最多可以切$w$刀。

她想总共切$K$刀，每刀要么竖着切要么横着切，如果竖着切了$i$刀，横着切了$j$刀，会得到$(i+1) × (j+1)$个巧克力，定义一个切$K$刀的方案的代价是每一刀切完后巧克力个数之和，假设每刀切的位置是随机选择的（即剩余能切的位置等概率随机选一个），请你求出期望代价，对$1e9+7$取模

$Solution:$

做法一:

参考xjh大佬的博客

我们把答案的每一部分分开来考虑

每一部分对答案的贡献就是这一部分能算进答案里的方案数$×$这部分的价值

显然这里的每一部分就指的是横着切$i$刀，竖着切$j$刀

这一部分的价值横着切i刀，竖着切j刀的价值很好求，就是$(i+1)(j+1)$

无论怎么切，这一部分的价值都是$(i+1)(j+1)$

难点在于求这一部分能算进答案里的方案数

我们把所有方案都画出来，就会清楚的发现怎么求了

方案数就是能走到这个状态的方案数$×$这个状态走到结束状态的方案数(简称来的状态和去的状态)

来的状态就是$A^i_h\times A^j_w\times$(不同的切横切竖的顺序),$A^i_h\times A^j_w$比较好理解，但对(不同的切横切竖的顺序) 不知道怎么求

我们稍微转换一下：有$i$个$0$(相当于横切)，$j$个$1$(相当于纵切)，问用它们构成一个长为$i+j$的$01$串的方案数，答案就相当于有$i+j$个位置，选$i$个位置放$0$,剩余位置放$1$的方案数，即$C^{i}_{i+j}$。

去的状态就是$A^{k-i-j}_{n-i-j}$

贴上$xjh$大佬的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
const int N=10005;
int h,w,k,n,ans,jc[N],inv[N];
int add(int a,int b)
{
    a+=b;
    if(a>=mod)a-=mod;
    return a;
}
int kuai(int a,int b)
{
    int res=1;
    while(b)
    {
        if(b%2==1)res=res*a%mod;
        a=a*a%mod;
        b=b/2;
    }
    return res;
}
signed main()
{
    freopen("ahri.in","r",stdin);
    freopen("ahri.out","w",stdout);
    jc[0]=1;inv[0]=inv[1]=1;
    for(int i=1;i<=10000;i++)jc[i]=jc[i-1]*i%mod;
    for(int i=2;i<=10000;i++)inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    for(int i=2;i<=10000;i++)inv[i]=inv[i]*inv[i-1]%mod;
    scanf("%lld%lld%lld",&h,&w,&k);
    n=h+w;
    for(int i=0;i<=h;i++)
        for(int j=0;j<=w;j++)
        {
            if(i==0&&j==0)continue;
            if(i+j>k)break;
            //ans=add(ans,a[h][i]*a[w][j]%mod*c[i+j][i]%mod*a[n-i-j][k-i-j]%mod*(i+1)%mod*(j+1)%mod);
            ans=add(ans,jc[h]*inv[h-i]%mod*jc[w]%mod*inv[w-j]%mod*jc[i+j]%mod*inv[i]%mod*inv[j]%mod*jc[n-i-j]%mod*inv[n-k]%mod*(i+1)%mod*(j+1)%mod);
        }
    cout<<(ans*kuai(jc[n]%mod*inv[n-k]%mod,mod-2)%mod+mod)%mod;
    return 0;
}

做法二:

概率期望$DP$(菜鸡我的做法)

下文中读入的$h,w$,分别设为$n,m$

设$g[i][j]$为切了$i$刀，有$j$刀是横向切的的期望,纵向切的刀数$k$显然$=i-j$

显然$g[i][j]=\sum f*val$,此处$f$表示其中一种切法的概率，$val$这种切法能得到的价值和。

我们去掉$val$,设$f[i][j]=\sum f$

对于$f$数组的转移显然不难,$f[i][j]=f[i-1][j]\times \dfrac{m-(k-1)}{n+m-i}+f[i-1][j]\times \dfrac{n-(j-1)}{n+m-i}$

但是$g$数组的转移就不简单了，我们考虑当前的$g[i][j]$如何从上一个状态转移过来。

之前说过$g[i][j]=\sum f*val$

$\qquad \qquad \qquad $$=f[i][j]\times (j+1)\times(k+1)$

我们假设

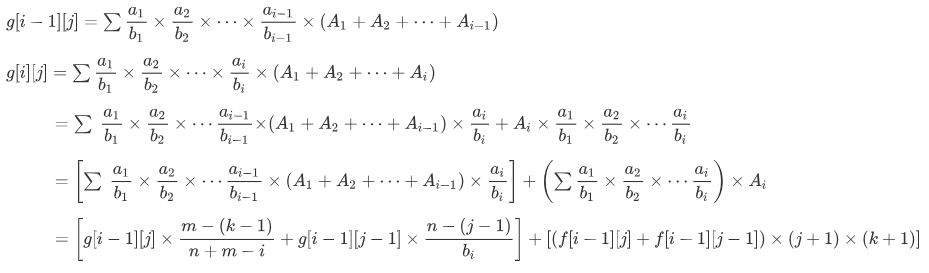
就这样，式子就推出来了

$ans=\sum\limits_{i=1}^{n} g[K][i]$

答案的寻找范围显然

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define int long long
#define re register
#define mod 1000000007
using namespace std;
inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
int g[2][5005],f[2][5005],ans,inv[10009];
signed main(){
    freopen("ahri.in", "r", stdin); freopen("ahri.out", "w", stdout); 
    int n=read(),m=read(),k=read();inv[0]=inv[1]=1;
    for (int i=2;i<=10007;++i)inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    f[1][1]=n*inv[n+m]%mod;f[1][0]=m*inv[n+m]%mod;//概率 
    g[1][1]=2*n%mod*inv[n+m]%mod;g[1][0]=2*m%mod*inv[n+m]%mod;//期望 
    for (int i=2;i<=k;++i){
        int now=i&1;//滚存 
        memset(f[now],0,sizeof(f[now]));
        memset(g[now],0,sizeof(g[now]));
        for (int j=0;j<=min(i,n);++j){
            if (i-j>m)continue;
            int k=i-j;
            //考虑最后一刀横向切还是纵向切
            int A=0,B=0; 
            if (k!=0){//最后一刀纵向切 
                A=f[now^1][j]*(m-(k-1))%mod*inv[n+m-i+1]%mod;
                g[now][j]+=g[now^1][j]*(m-(k-1))%mod*inv[n+m-i+1]%mod+(j+1)*(k+1)%mod*A%mod;
            }
            f[now][j]%=mod;g[now][j]%=mod;
            if (j!=0){//最后一刀横向切 
                B=f[now^1][j-1]*(n-(j-1))%mod*inv[n+m-i+1]%mod;
                g[now][j]+=g[now^1][j-1]*(n-(j-1))%mod*inv[n+m-i+1]%mod+(j+1)*(k+1)%mod*B%mod;
            }
            f[now][j]=A+B;//概率相加 
            f[now][j]%=mod;g[now][j]%=mod;
        }
    }
    for (int i=0;i<=n;++i)
        ans=(ans+g[k&1][i])%mod;//统计答案 
    cout<<ans<<endl;
}

其他做法

此外还有复杂度跟我的做法一样，但实现更简单一些的$DP$;

并且用$FFT$优化$xjh$大佬的$O(nlogn)$做法和一种$O(logK+logn+logm)$的神奇做法。